Computational Toolsmiths Logo Image Computational Toolsmiths
Software Tools for Computational Science, Engineering, and Medicine

WavBox Software Library

Summary of the WavBox Software Library

The WavBox Software logo image, shown above, is displayed as a "splash screen" image on start-up of the software. This composite image logo has been designed to reveal some of the fundamental aspects of wavelet transforms. It shows the most famous Daubechies wavelets (those corresponding to filters with four coefficients) and the characteristic tiling of the time-frequency plane with tall thin tiles at high frequencies and short fat tiles at low frequencies.

WavBox Software (Toolsmiths Wavelet Toolbox) is

  • the original MATLAB Wavelet Toolbox,
  • the first available as free software in 1991, and
  • the first available as commercial software in 1994.

WavBox Software Version 4.6 is compatible with MATLAB 7, 8 and 9. A brief summary of WavBox Software follows below:

WavBox 4.6 - A Software Toolbox for Wavelet Transforms and Adaptive Wavelet Packet Decompositions with FirWav Filter Library

WavBox Software provides both a function library and a computing environment for wavelet transforms and adaptive wavelet packet decompositions. The software package contains 317 MATLAB m-files (approximately 1.4 MB uncompressed) implementing an extensive collection of these wavelet transforms, expansions, decompositions, wavelet filters, wavelets, and related functions. This function library performs multiresolution analyses of 1-D multichannel signals and 2-D images for arbitrary length and size data. MATLAB is a technical computing environment available from The MathWorks Inc.

WavBox Software includes: continuous wavelet transform valid for all wavelets including the complex Morlet, real Gabor, Meyer, and Mexican hat wavelets; overscaled pyramid transforms, discrete wavelet transforms, and adaptive wavelet and cosine packet decompositions by best basis and matching pursuit (Mallat, Coifman, Wickerhauser, and other authors); satisficing search algorithms for the selection of near-best basis decompositions with either additive or non-additive information costs (Taswell); the systematized collection of FIR wavelet filters computable by spectral factorization of the Daubechies polynomial (Taswell); empirical tests for evaluating the parameters of multi-rate filter banks (Taswell); wavelet shrinkage denoising methods (Donoho and Johnstone); the fast wavelet based numerical methods (Beylkin et al) for the implementation of fast matrix multiplication and solution of linear systems in the wavelet domain. These latter methods can be used to implement pseudo-differential and integral operators.

Various choices of filter classes (orthogonal, biorthogonal, etc), filter families (least-asymmetric, most-symmetric, etc), and convolution versions (interval, circular, extended, etc) exist for each transform, expansion, and decomposition. The software has been designed for efficient automated computation, interactive exploratory data analysis, and pedagogy. Essential features of the design include: perfect reconstruction for multiresolution decomposition of data of arbitrary size not restricted to powers of 2; both command line and graphical user interfaces with a comprehensive set of plots and visual displays; an object property expert system with artificial intelligence for configuring valid property combinations; heirarchical modules and switch-driven function suites; vector-filter and matrix-operator implementations of convolutions; extensibility for the inclusion of other wavelet filters, convolution versions, and transforms; optional arguments with built-in defaults for most m-files; and extensive on-line help and self-running tutorial demos.

Endorsements from WavBox Software Users

The endorsements summarized below were received from users who were describing their experience with various versions of WavBox Software as reflected in the internet email date-time stamps of their quotes.

  • The function library included in WavBox Software... (Toolsmiths Wavelet Toolbox) ...provides a significantly richer set of tools than that found in the MathWorks Wavelet Toolbox, particularly in the adaptive wavelet packet areas. This feature is absolutely essential in dealing with real-world problems.
    Date: Thu, 22 May 1997 16:22:37 -0700 (PDT); From: rluppold@westol.com;
    Rob Luppold, President, Luppold & Associates Inc, 303 East Main Street, West Newton, PA 15089.
  • Excellent and at highest professional level. I can hardly imagine to be able to find better software.
    Date: Fri, 2 May 1997 13:05:23 +0200 (MET DST); From: vesely@math.muni.cz;
    Prof. Vesely Vitezslav, Department of Applied Mathematics, Masaryk University of Brno, Czech Republic.
  • 1) WavBox Software is the most comprehensive wavelet package written for Matlab: while other packages can offer the basic wavelet transform algorithm, only in WavBox you can find a variety of wavelet filters, wavelet packet cost functions, and edge adapted algorithms which are no where else. 2) WavBox is very efficient in terms of the implementation of the algorithms, thus, it can process 2 dimensional images quite fast. 3) The window based WavBox program makes it easy to learn and use the basic concepts of the wavelet transform and results fast. 4) The code is clearly written and documented, so when I had to make a modification to one of the algorithms, it didn't take me very long to figure how to do it.
    Date: Sun, 29 Oct 1995 20:06:43 +0200 (IST); From: armin@eng.tau.ac.il;
    Armin Shmilovici, Department of Industrial Engineering, Tel-Aviv University, 69978 Tel-Aviv, Israel.
  • We have had WavBox for almost a year and have used it extensively in modeling speech vectors. It has proven to be both a useful research tool, saving many hours of programing time, but also invaluable in bringing new personnel up to speed using a tutorial developed in-house. It is an excellent addition to the Signal Processing Toolbox.
    Date: Wed, 25 Oct 1995 10:48:03 -0700; From: carmody@mml.mmc.com;
    Dr. J. C. Carmody, Scientist, Speech and Signal Processing, Martin Marietta Laboratories, 9425 Dunloggin Road, Ellicott City, Maryland 21042-5115.
  • Since I received WavBox 4.1b, I have employed it to transform a variety of signals. Its functions and user friendly interface by means of Matlab are impressive. I have some other software to perform wavelet analysis such as TeachWave... (now called WaveLab, Dept of Statistics, Stanford Univ), ...Wavelet Transform by Mac Cody, and others. WavBox is superior to them. I don't regret that I spend a little fee to pay this fabulous software WavBox. Now I completely switch to WavBox to do all my research related to wavelet analysis. I really enjoy using it.
    Date: Thu Sep 15 21:23:44 1994; From: hongbosu@ksu.ksu.edu;
    Hong-Bo Su, Department of Chemical Engineering, Kansas State University, Manhattan, KS 66506-5102
  • A very useful tool for anyone involved in the wavelet field. An impressive array of wavelet analysis, synthesis and display techniques.
    Date: Sun Sep 11 17:34:10 1994;
    Graduate student.
  • An excellent tool for education and research. Thank you again and congratulations.
    Date: Mon Sep 5 07:35:50 1994; From: Anestis.Antoniadis@imag.fr;
    Professor Anestis Antoniadis, Laboratoire IMAG-LMC, University of Grenoble I, B.P. 53 X, F-38041 Grenoble Cedex FRANCE.
  • WavBox is the most complete collection of Matlab routines for computation and visual display that I have come accross.
    Date: Sun Aug 28 07:51:17 1994; From: srini@wuche2.wustl.edu;
    Srinivas Palavajjhala, Department of Chemical Engineering, Washington University, St. Louis, MO 63130-4899.
  • It is very impressive. I think this package is one of the best software I ever used. I did not have any problem to get it up and running. It does as it is supposed to do. It covers most functions people expect from wavelets.
    Date: Mon, 27 Dec 93 08:50:36 -0800; From: kuo@h3912.chinalake.navy.mil;
    Wei Kuo, Naval Air Warfare Center Weapons Division, EO Missile Systems Branch Code C2912, China Lake, CA 93555-6001.

Continuous Wavelet Transform

To demonstrate the continous wavelet transform, consider the following test signal called "spires" which has peak-like transients:

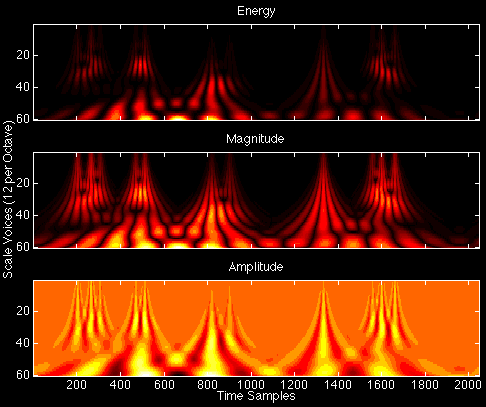
Transforming the spires signal with Gabor real nonorthogonal symmetric wavelets produces the following images in the time-scale transform domain for energy and magnitude of the transform coefficients:

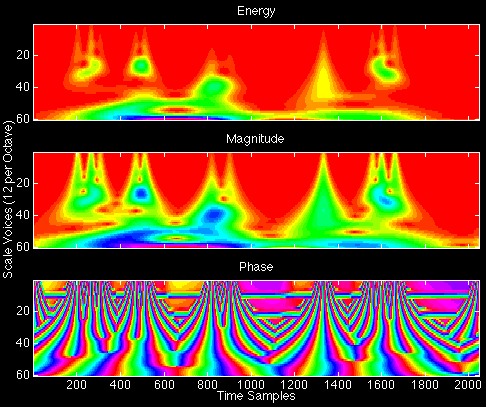
Transforming the spires signal with Morlet complex nonorthogonal symmetric wavelets produces the following images in the time-scale transform domain for energy, magnitude, and phase of the transform coefficients:

Here are plots of the real and imaginary parts of the Morlet complex nonorthogonal symmetric wavelets used in the above continous wavelet transform with 12 scale voices per octave:

Comparison of Continuous, Nonsubsampled, and Discrete Wavelet Transforms

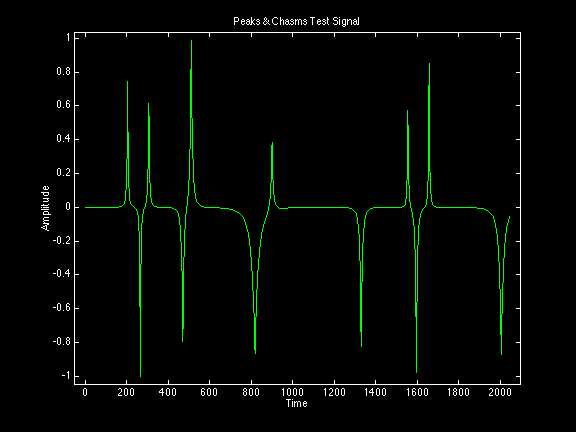
For the comparison of the different transforms, the same test signal is used in the following sequence of plots. This test signal is the "peaks & chasms" test signal. It is a variation of the "spires" test signal with both positive and negative peak-like transients:

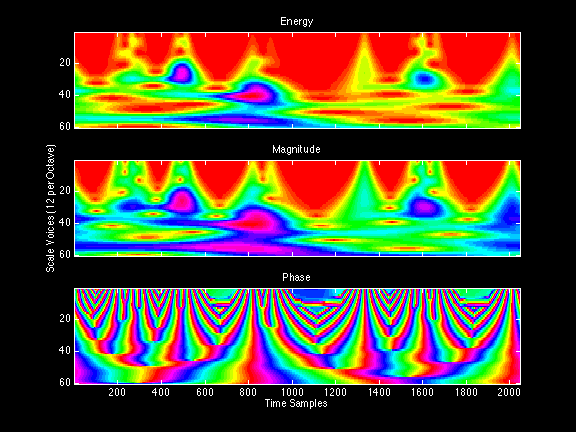
Continuous wavelet transform with Morlet complex nonorthogonal symmetric wavelets, and a periodized frequency domain convolution with a peak near-aligned phase shift:

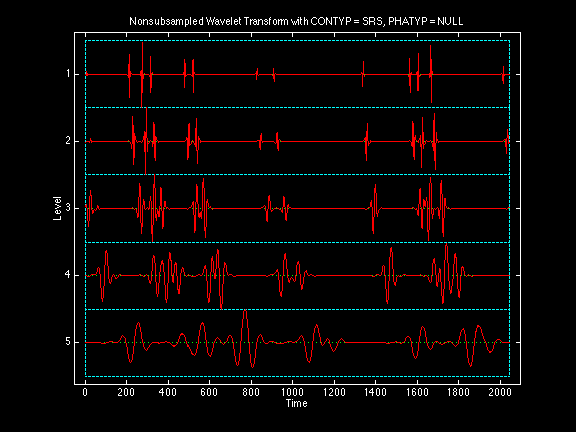
Nonsubsampled wavelet transform with Daubechies Real Biorthogonal symmetric balanced Most Regular DRBMR(10,10;5,5) wavelets, and a periodized frequency domain convolution with a peak near-aligned phase shift (anti-causal):

Nonsubsampled wavelet transform with DRBMR(10,10;5,5) wavelets, and a doubly-periodized time domain convolution for symmetrically-reflected signal ends with a peak non-aligned phase shift (causal):

Discrete wavelet transform with DRBMR(10,10;5,5) wavelets, and a doubly-periodized time domain convolution for symmetrically-reflected signal ends with a peak near-aligned phase shift (anti-causal, compatible with FBI fingerprint image compression standard):

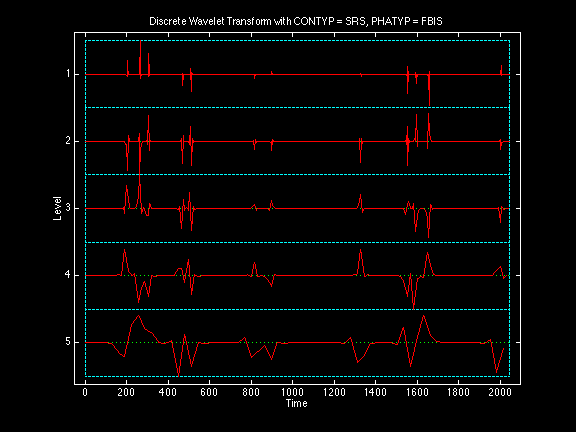
Note that the nonsubsampled wavelet transform is an oversampled transform with the same number of data points in each level of the transform domain as in the signal domain. However, the discrete wavelet transform is a critically sampled transform with same number of data points in both signal and transform domains because the number of data points is halved at each level in the transform domain. (For display purposes, the data points are connected by linear interpolation.)

Comparison of Wavelet and Cosine Packet Decompositions

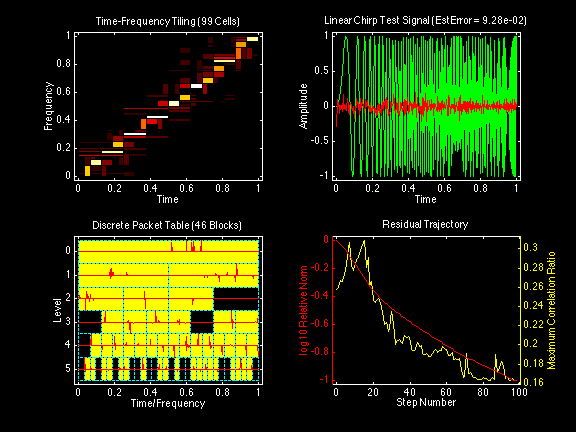
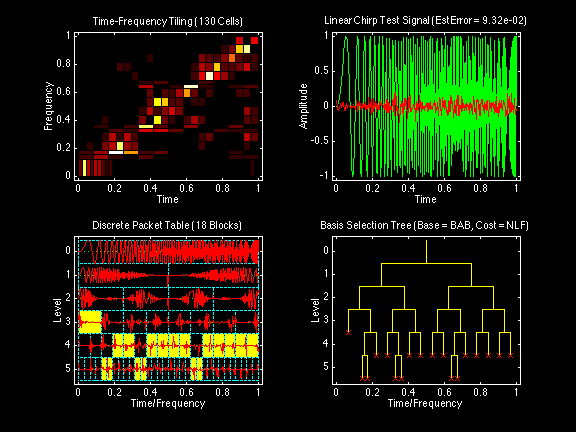
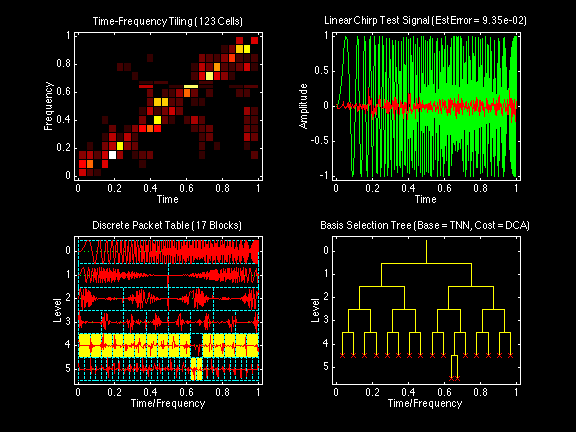
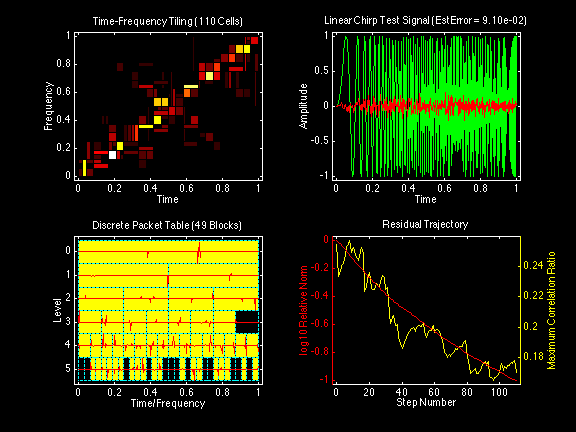
All wavelet and cosine packet decompositions displayed in the following sequence of figures were computed on the same "Linear Chirp" test signal. This linear chirp test signal has been designed to yield a diagonal band of tiles from the origin (0,0) to the point (1,1) in a time-frequency tiling plot with both time and frequency normalized to the interval [0,1].

All of the wavelet packet decompositions used the same Daubechies Real Orthogonal Least-Asymmetric DROLA(6;3) filter bank with the same boundary-adjusted convolution. Reconstruction error estimates were based on reconstruction of the signal from a number of transform coefficients constituting 99% of the energy of the signal.

For various references, see the Papers Page. In particular, note the article Satisficing Search Algorithms for Selecting Near-Best Bases in Adaptive Tree-Structured Wavelet Transforms published in IEEE Transactions on Signal Processing, October 1996, Vol 44 No 10 pages 2423-2438.

Wavelet packet decomposition by bottom-up tree search with additive information cost function:

Wavelet packet decomposition by top-down tree search with non-additive information cost function:

Wavelet packet decomposition by matching pursuit search:

Cosine packet decomposition by bottom-up tree search with additive information cost function:

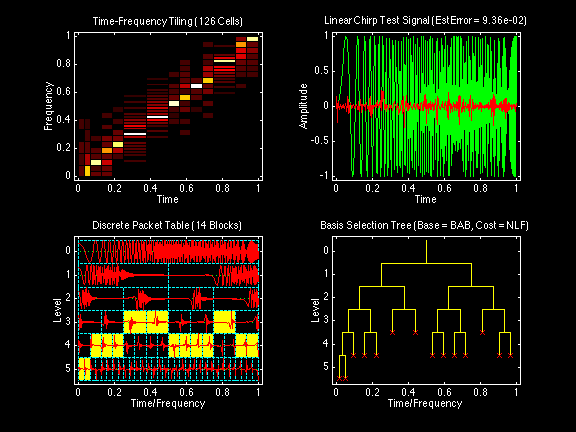
Cosine packet decomposition by top-down tree search with non-additive information cost function:

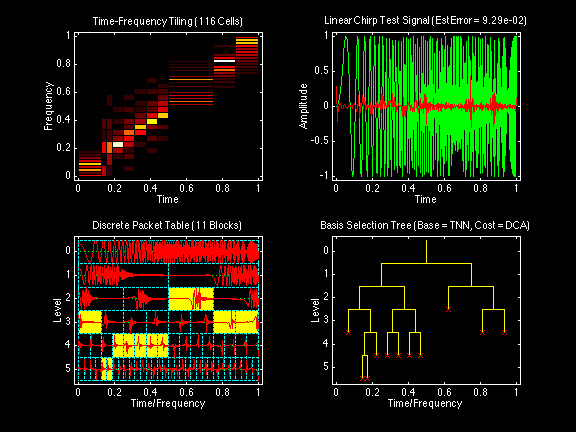
Cosine packet decomposition by matching pursuit search: